启发式搜索：A* 算法与八数码问题探究

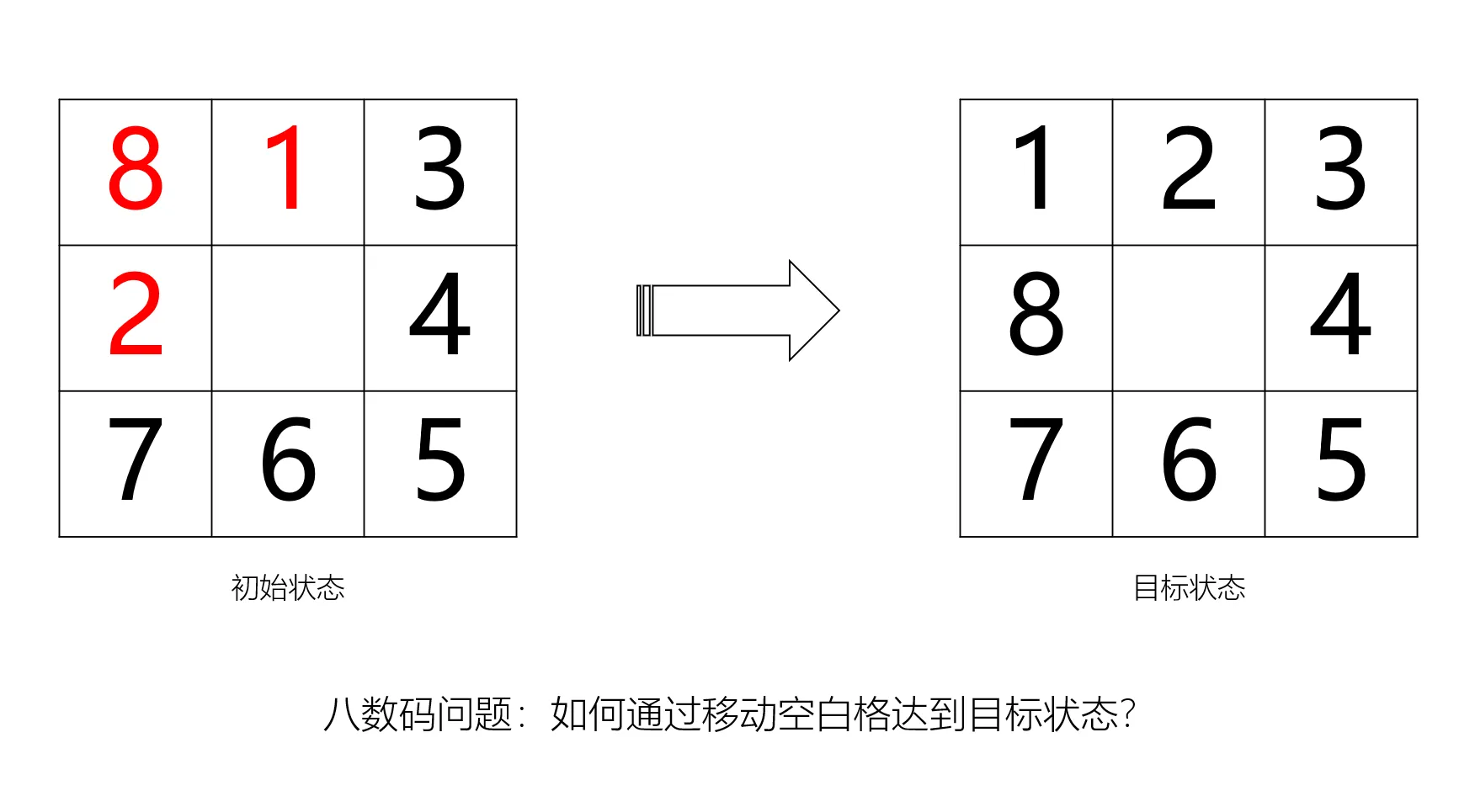
在一个$3 \times 3$的棋盘中，存在编号为1~8或空白的共9种格子。给定一种状态，只允许移动空白格，应该通过何种路径达到目标状态呢？

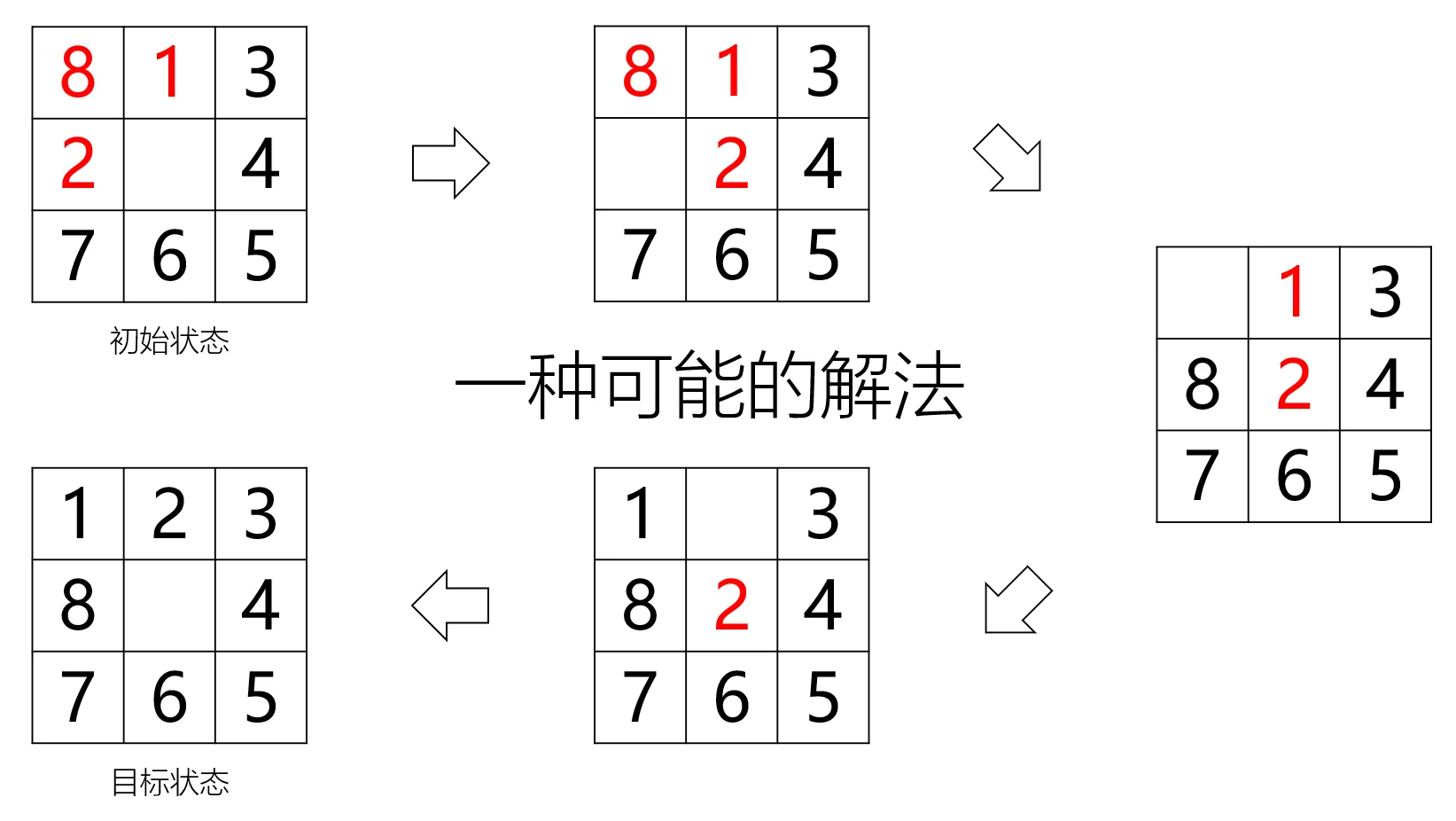
解决思路

以初始状态为起点进行搜索，应用三种搜索算法：BFS, DFS, A*

判断目标状态是否可达：逆序和奇偶性相同即可达

将每种状态看作一个节点，可以使用盲目搜索算法进行遍历，找到目标状态为止。由于状态空间的庞大（指数级），需要对状态进行查重筛检，这就使得算法的效率不尽人意，因此引入了启发式搜索的A*算法。A*算法使用一个人为定义的估值函数来估算每种状态的“距离”，从而使得不同状态之间的优劣得以区分，把无权图遍历问题转化为了有权图的最短路径问题，搜索效率得到了极大的提升。

由此看来，A*算法最重要的部分便是估值算法的设计。对于八数码问题，经典的两种估值算法分别为：

1. 不在正确位置的数字个数
2. 每个数字到其正确位置的距离的和，称为曼哈顿距离

相比较而言曼哈顿距离显然包含了更多信息，因此针对本问题我选择了曼哈顿距离作为估值函数。

但是估值终究是估值，A*算法通过距离估值可以少走弯路，尽力而为地找到一个优解，但很可能并不是最优解。

解决方案

• 语言：C++
• 状态节点：用string类型存储，便于收集与比对，用-表示空白格
• 查重集：unordered_map(C++11)，内部实现为散列表
• 队列与栈：vector实现，由于需要回溯，便手动操作Push与Pop
• 查找计时：ctime
• 环境：CLion 2019.3（G++ 8.2.1 x64）

广度优先搜索

BFS访问遍历所有出现的节点，复杂度轻易地达到了指数级。对于变化次数较多的序列，如果使用BFS进行遍历的话，时间复杂度是有些不可接受的。

为了解决以上问题，修改了查重算法，选择使用散列表实现的unordered_map来进行查重，使得该算法的效率得到了极大的提升。

BFS的最大优势是寻找到的解必为最优解之一，因此将BFS得到的深度作为后面的标准深度。

实验记录

实验样本	深度	遍历次数	耗时/s
“134-85726”	7	166	0.03
“5674-8321”	30	181358	0.557
“-75168324”	28	179983	0.628
“32841-567”	29	180492	0.532
“32-418567”	30	181228	0.535

Source Code

点击展开

#include <iostream>
#include <string>
#include <vector>
#include <ctime>
#include <unordered_map>

using namespace std;
struct node {
    string s;
    int ptr, pre, depth;
};

node ori;
node des;
vector<node> q;
unordered_map<string, bool> visited;
int times = 0;

void init() {
    ori.s = "5674-8321";
    for (int i = 0; i < ori.s.length(); i++) {
        if (ori.s[i] == '-') {
            ori.ptr = i;
            break;
        }
    }
    ori.pre = -1;
    ori.depth = 0;
    des.s = "1238-4765";
    des.ptr = 4;
}

bool check(string s) {
    int sum = 0;
    for (int j = 0; j < s.length(); j++) {
        for (int w = 0; w < j; w++) {
            if (s[w] != '-' && s[j] != '-' && s[w] > s[j]) {
                sum++;
            }
        }
    }
    if (sum % 2 == 0) {
        return true;

    }
    else {
        return false;
    }
}

bool isVisited(node& n) {
    if (visited.count(n.s) == 0) {
        return false;
    }
    return true;
}

node swap(node n, const int a, const int b) {
    char temp = n.s[a];
    n.s[a] = n.s[b];
    n.s[b] = temp;
    n.ptr = n.s[a] == '-' ? a : b;
    n.depth++;
    return n;
}

void process(int front, int arg) {
    node temp = swap(q[front], q[front].ptr, q[front].ptr + arg);
    temp.pre = front;
    if (!isVisited(temp)) {
        visited[temp.s] = true;
        q.push_back(temp);
    }
}

void up(int front) {
    if (q[front].ptr - 3 >= 0) {
        process(front, -3);
    }
}

void down(int front) {
    if (q[front].ptr + 3 <= 8) {
        process(front, 3);
    }
}

void left(int front) {
    int ptr = q[front].ptr;
    if (ptr != 0 && ptr != 3 && ptr != 6) {
        process(front, -1);
    }
}

void right(int front) {
    int ptr = q[front].ptr;
    if (ptr != 2 && ptr != 5 && ptr != 8) {
        process(front, 1);
    }
}

void show(node& n) {
    cout << "Found" << endl;
    vector<node> ans;
    while (n.pre != -1) {
        ans.push_back(n);
        n = q[n.pre];
    }
    ans.push_back(ori);
    for (auto it = ans.rbegin(); it != ans.rend(); it++) {
        cout << "--------- Depth = " << it->depth << endl;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                cout << it->s[3 * i + j] << "  ";
            }
            cout << endl;
        }
    }
    cout << "Total times: " << times << endl;
}

int main() {
    clock_t start = clock();
    init();
    if (check(ori.s) != check(des.s)) {
        cout << "No solution" << endl;
        return 0;
    }
    q.push_back(ori);
    for (int front = 0; front < q.size(); front++) {
        times++;
        if (q[front].s == des.s) {
            show(q[front]);
            break;
        }
        left(front);
        up(front);
        right(front);
        down(front);
    }
    clock_t end = clock();
    cout << "Total cost: " << (double)(end - start) / CLOCKS_PER_SEC << " second" << endl;
    return 0;
}

深度优先搜索

没有边界终止条件，永远可以往下走

手动设置递归深度，如果没有事先知道递归深度大概范围的话，查找效率是非常低的。

为什么有些解找不到？

把遍历过的所有状态全部置入查重集，会导致这种情况：后面路径的节点已经被前面路径置入查重集，导致前面路径因为递归深度而终止，后面路径因为查重而终止，找不到目标解。当递归深度较深时尤其明显。

遂修正查重算法，只保留这条路自己遍历过的节点，也就是说只保证当前路不走回头路。这样便保证了有解且无需回溯寻找路径。同时查重集最大容量即为递归深度，大大优化了空间与时间复杂度。

递归深度为$N$

则全集查重
$$
最差情况时间复杂度=O(4^{2N})
$$

$$
空间复杂度=O(4^N)
$$

单线查重
$$
最差情况时间复杂度=O(N×4^N)
$$

$$
空间复杂度=O(N)
$$

由于时间复杂度为$O(4^N)$级别，深度较大时需手动设置递归边界，即找到一个解后退出递归。

由此带来了新的问题如下。

有多种路径可以达到目标状态，如何择优？

尝试：

由

- 7 5

1 6 8

3 2 4

到

1 2 3

8 - 4

7 6 5

最大递归深度为30

实验结果：

运行2 ~ 3分钟（约查找$10^{8}$次），共得到12个解，如下:

Depth	Count
28	2
30	10

从结果来看，对于不同的解出现了不同的深度——由此我们得到两点结论：

• 八数码问题的解不是唯一的
• 在深度优先搜索中大部分解往往逼近于递归深度

如果对30层递归深度的全集进行搜索的话，总遍历次数需要达到$4^{30}$，这是非常恐怖的：
$$
4^{30}=1,152,921,504,606,846,976=1.15E18
$$

从理论上要得到所有解并择优需要的时间代价是不可接受的，我们难以得到最理想的答案。

因此，高深度情况下，DFS在理想时间内只能得到解，得不到最优解。

该算法的效率及成功率很大程度上取决于递归深度的设定，若事先不知道理论深度，人为定义的最大递归深度与理论深度差距较大时，得到的解与最优解会相差极大，当设置的最大深度小于理论深度时甚至会无解。

那DFS是不是一无是处呢？

显然深度优先搜索最大的优势就是极低的空间复杂度，然而因为需要遍历的总量不多（去重后），这个特性在八数码问题上并没有显示出优势，不过可以为大规模数据运算提供另一种低成本的思路。

综上，在解决八数码问题上，DFS并不是一种优秀的算法。

实验记录

设置最大递归深度为32

实验样本	理论深度	寻找深度	遍历次数	耗时/s
“134-85726”	7	31	203512	0.431
“5674-8321”	30	32	188739	0.352
“-75168324”	28	32	1867331	2.386
“32841-567”	29	31	871753	1.213
“32-418567”	30	32	1015214	1.511

Source Code

点击展开

#include <iostream>
#include <string>
#include <vector>
#include <unordered_map>
#include <ctime>

using namespace std;
struct node {
    string s;
    int ptr;
};
//最大递归深度
const int maxDepth = 33;
int times = 0;
bool isFound = false;

node ori;
node des;
vector<node> stack;
unordered_map<string, bool> visited;

void dfs(node n, int count);

void init() {
    ori.s = "5674-8321";
    for (int i = 0; i < ori.s.length(); i++) {
        if (ori.s[i] == '-') {
            ori.ptr = i;
            break;
        }
    }
    des.s = "1238-4765";
    des.ptr = 4;
    stack.push_back(ori);
}

bool check(string s) {
    int sum = 0;
    for (int j = 0; j < s.length(); j++) {
        for (int w = 0; w < j; w++) {
            if (s[w] != '-' && s[j] != '-' && s[w] > s[j]) {
                sum++;
            }
        }
    }
    if (sum % 2 == 0) {
        return true;
    }
    else {
        return false;
    }
}

node swap(node& n, const int a, const int b) {
    node next = n;
    char temp = next.s[a];
    next.s[a] = next.s[b];
    next.s[b] = temp;
    next.ptr = next.s[a] == '-' ? a : b;
    return next;
}

bool isVisited(node& n) {
    if (visited.count(n.s) == 0) {
        return false;
    }
    return true;
}

void process(node& n, int arg, int count) {
    node temp = swap(n, n.ptr, n.ptr + arg);
    if (!isFound && !isVisited(temp) && count < maxDepth) {
        stack.push_back(temp);
        visited[temp.s] = true;
        dfs(temp, count + 1);
        stack.pop_back();
        visited.erase(temp.s);
    }
}

void up(node& n, int count) {
    if (n.ptr - 3 >= 0) {
        process(n, -3, count);
    }
}

void down(node& n, int count) {
    if (n.ptr + 3 <= 8) {
        process(n, 3, count);
    }
}

void left(node& n, int count) {
    int ptr = n.ptr;
    if (ptr != 0 && ptr != 3 && ptr != 6) {
        process(n, -1, count);
    }
}

void right(node& n, int count) {
    int ptr = n.ptr;
    if (ptr != 2 && ptr != 5 && ptr != 8) {
        process(n, 1, count);
    }
}

void show(node* n) {
    cout << "Found" << endl;
    int depth = 0;
    for (auto it = stack.begin(); it != stack.end(); it++) {
        cout << "--------- Depth = " << depth++ << endl;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                cout << it->s[3 * i + j] << "  ";
            }
            cout << endl;
        }
    }
}

void dfs(node n, int count) {
    if (n.s == des.s) {
        isFound = true;
        show(&n);
        return;
    }
    times++;
    left(n, count);
    up(n, count);
    right(n, count);
    down(n, count);
}

int main() {
    clock_t start = clock();
    init();
    if (check(ori.s) != check(des.s)) {
        cout << "No solution" << endl;
        return 0;
    }
    dfs(ori, 0);
    clock_t end = clock();
    cout << "Total times = " << times << endl;
    cout << "Total cost: " << (double)(end - start) / CLOCKS_PER_SEC << " second" << endl;
    return 0;
}

A*

如何优化A*算法的效率？

采用曼哈顿距离（每个点当前位置与理想位置需移动步数之和）来代替不在理想位置的点的个数，可以得到更加准确的估值函数。

估值函数确定之后，剩下的就是通过Dijkstra来寻找最短路径的问题了。

需求如下：

• 储存每一个访问过的节点，以便回溯路径
• 对于每一个当前访问的点，与被访问过的所有点进行查重校检
• 对于队列中所有即将要访问的点，取出估值最小的点进行访问

方案如下：

• 队列与存储：建立一个队列用来储存所有的节点，用一个指针指向队头元素，每次循环使指针向后移动一位，保证指针始终指向当前访问节点。队列不执行pop操作，从队头到指针的所有元素全部保留在原位以便回溯。遍历得到的将要访问的结点从队尾压入队列。
• 查重校检：取队头直到当前元素建立哈希表查重（unordered_map(C++11))，并且访问每一个结点后都将该节点的指针（节省内存）放入哈希表中。
• 估值：对每个状态进行估值并存储在状态结构体中，每个状态仅估值一次。
• 取最小值：对当前节点到队尾建立最小堆，有以下特性：
  • 每次取堆顶节点即为最小值
  • 每压入一个节点进行最小堆化
  • 每次堆维护时间复杂度为$O(logN)$
  • 堆建立在队列中，不额外占用内存

最终得到算法的时间复杂度为
$$
O(N+NlogN)
$$
空间复杂度为
$$
O(N)
$$
N为遍历的节点个数，通常小于$10^5$

通过优化的A*对样本进行测试，得到的实验结果令人欣喜，准确率与效率都非常高。

实验记录

实验样本	理论深度	寻找深度	遍历次数	耗时/s
“134-85726”	7	7	9	0.051
“5674-8321”	30	30	5691	0.189
“-75168324”	28	28	8152	0.194
“32841-567”	29	29	12747	0.219
“32-418567”	30	30	18765	0.296

Source Code

点击展开

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <unordered_map>
#include <ctime>
#include <cmath>

using namespace std;
struct node {
    string s;
    int ptr, pre, F, depth;
};

node ori;
node des;
unordered_map<char, int> pos;
unordered_map<string, bool> visited;
vector<node> q;
int times = 0;


bool cmp(const node& a, const node& b) {
    return a.F > b.F;
}

int H(node& n) {
    int H = 0;
    for (int i = 0; i < n.s.length(); i++) {
        if (n.s[i] != des.s[i]) {
            H += fabs(i % 3 - pos[n.s[i]] % 3) + fabs(i / 3 - pos[n.s[i]] / 3);
        }
    }
    return H;
}

int F(node& n) {
    return H(n) + n.depth;
}

bool check(string s) {
    int sum = 0;
    for (int j = 0; j < s.length(); j++) {
        for (int w = 0; w < j; w++) {
            if (s[w] != '-' && s[j] != '-' && s[w] > s[j]) {
                sum++;
            }
        }
    }
    if (sum % 2 == 0) {
        return true;
    }
    else {
        return false;
    }
}

void init() {
    des.s = "1238-4765";
    des.ptr = 4;
    for (int i = 0; i < des.s.length(); i++) {
        pos[des.s[i]] = i;
    }
    ori.s = "5674283-1";
    for (int i = 0; i < ori.s.length(); i++) {
        if (ori.s[i] == '-') {
            ori.ptr = i;
            break;
        }
    }
    ori.pre = -1;
    ori.depth = 0;
    ori.F = F(ori);
}

bool isVisited(node& n) {
    if (visited.count(n.s) == 0) {
        return false;
    }
    return true;
}

node swap(node n, const int a, const int b) {
    char temp = n.s[a];
    n.s[a] = n.s[b];
    n.s[b] = temp;
    n.ptr = n.s[a] == '-' ? a : b;
    n.depth++;
    return n;
}

void process(int front, int arg) {
    node temp = swap(q[front], q[front].ptr, q[front].ptr + arg);
    temp.pre = front;
    if (!isVisited(temp)) {
        visited[temp.s] = true;
        temp.F = F(temp);
        q.push_back(temp);
        push_heap(q.begin() + front + 1, q.end(), cmp);
    }
}

void up(int front) {
    if (q[front].ptr - 3 >= 0) {
        process(front, -3);
    }
}

void down(int front) {
    if (q[front].ptr + 3 <= 8) {
        process(front, 3);
    }
}

void left(int front) {
    int ptr = q[front].ptr;
    if (ptr != 0 && ptr != 3 && ptr != 6) {
        process(front, -1);
    }
}

void right(int front) {
    int ptr = q[front].ptr;
    if (ptr != 2 && ptr != 5 && ptr != 8) {
        process(front, 1);
    }
}

void show(node& n) {
    cout << "Found" << endl;
    vector<node> ans;
    while (n.pre != -1) {
        ans.push_back(n);
        n = q[n.pre];
    }
    ans.push_back(ori);
    for (auto it = ans.rbegin(); it != ans.rend(); it++) {
        printf("--------- Depth = %d, F = %d\n", it->depth, it->F);
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                cout << it->s[3 * i + j] << "  ";
            }
            cout << endl;
        }
    }
    cout << "Total times: " << times << endl;
}

int main() {
    clock_t start = clock();
    init();
    if (check(ori.s) != check(des.s)) {
        cout << "No solution" << endl;
        return 0;
    }
    q.push_back(ori);
    make_heap(q.begin(), q.end(), cmp);
    for (int front = 0; front < q.size(); front++) {
        times++;
        if (q[front].s == des.s) {
            show(q[front]);
            break;
        }
        left(front);
        up(front);
        right(front);
        down(front);
    }
    clock_t end = clock();
    cout << "Total cost: " << (double)(end - start) / CLOCKS_PER_SEC << " second" << endl;
    return 0;
}

八数码问题深度是否存在极限？

国际魔方协会认为打乱三阶魔方只需要精心计算的二十步，此时魔方处于“最混乱”的状态，任何操作都属于将魔方复原的第一步，因此魔方的“20”被称为“上帝之数”。

回到八数码问题，通过DFS输出深度大于某阈值的排列组合，我将阈值深度设置为100层，取1000个样本进行Astar查找，发现多数样本仅二十多步即可还原。步数最多的为30步，而且他们全部都有一个共同的特点——顺序上大致是目标状态的逆序。

曼哈顿距离

指所有节点当前位置到理想位置的距离的和

既然估值函数是通过曼哈顿距离来确定的，那曼哈顿距离最大的状态就是启发式算法极力避免去访问的节点，换句话说，曼哈顿距离最大的状态是不是最为“混乱”的状态呢？

两种状态：

• 先确保角上节点的距离：角节点为4，边界点为2，曼哈顿距离为24
• 所有节点平均：角节点和边界点均为3，曼哈顿距离为24

提出一个设想：

当曼哈顿距离达到24时，深度（可能）会达到30，那么30是否是深度的极限呢？

但实验结果表明两者并没有非常直接的关系，水平有限，暂无法从数学上给出证明。

想要知道答案，需要用BFS算法跑到第31层看一看。

//令起点为目标状态
ori.s = "1238-4765";

在这里说一下我的代码中对于深度的定义：初始状态深度为0，每移动一次深度+1

在BFS中加入几行测试代码使程序输出所有深度大于等于30的状态：

//H为计算曼哈顿距离的函数
if (q[front].depth >= 30) {
    cout << q[front].s << " Depth = " << q[front].depth <<" H = "<<H(q[front])<< endl;
}

程序输出为：

点击展开

2874-6351 Depth = 30 H = 20
5426-8371 Depth = 30 H = 20
-47528361 Depth = 30 H = 22
-87456321 Depth = 30 H = 24
4875-6321 Depth = 30 H = 24
5486-7321 Depth = 30 H = 24
58-437621 Depth = 30 H = 22
54-678321 Depth = 30 H = 24
5416-8327 Depth = 30 H = 20
1874-6325 Depth = 30 H = 16
321458-67 Depth = 30 H = 14
32147856- Depth = 30 H = 14
187236-45 Depth = 30 H = 16
4675-1328 Depth = 30 H = 24
5314-8627 Depth = 30 H = 16
-21438567 Depth = 30 H = 14
5324-8671 Depth = 30 H = 16
5278-4361 Depth = 30 H = 16
3174-8526 Depth = 30 H = 16
5374-2681 Depth = 30 H = 20
5647-8123 Depth = 30 H = 16
564278-31 Depth = 30 H = 22
-67258341 Depth = 30 H = 24
6572-8341 Depth = 30 H = 24
7654-3821 Depth = 30 H = 16
5476-3821 Depth = 30 H = 20
421538-67 Depth = 30 H = 16
5647-2381 Depth = 30 H = 20
5647-3821 Depth = 30 H = 16
-43652781 Depth = 30 H = 16
5214-8367 Depth = 30 H = 16
3674-2581 Depth = 30 H = 20
5672-4381 Depth = 30 H = 22
541628-37 Depth = 30 H = 20
543672-81 Depth = 30 H = 20
54-632781 Depth = 30 H = 20
2614-8357 Depth = 30 H = 16
18-276345 Depth = 30 H = 16
18725634- Depth = 30 H = 20
-87216345 Depth = 30 H = 20
5612-8347 Depth = 30 H = 20
32-418567 Depth = 30 H = 14
58-467231 Depth = 30 H = 24
58-427361 Depth = 30 H = 22
8672-5341 Depth = 30 H = 20
5172-8346 Depth = 30 H = 20
2174-8356 Depth = 30 H = 16
3874-6521 Depth = 30 H = 20
-57684321 Depth = 30 H = 22
547638-21 Depth = 30 H = 24
5476-8231 Depth = 30 H = 24
7654-2381 Depth = 30 H = 20
765342-81 Depth = 30 H = 20
1672-8345 Depth = 30 H = 16
5472-8361 Depth = 30 H = 22
5476-8123 Depth = 30 H = 20
3274-8561 Depth = 30 H = 16
5276-8341 Depth = 30 H = 22
576328-41 Depth = 30 H = 24
5764-8231 Depth = 30 H = 24
5436-8721 Depth = 30 H = 16
58-367421 Depth = 30 H = 24
5683-7421 Depth = 30 H = 24
58741632- Depth = 30 H = 24
5674-8321 Depth = 30 H = 24
-47518326 Depth = 30 H = 22
5478-6321 Depth = 30 H = 22
57-846321 Depth = 30 H = 22
7658-4321 Depth = 30 H = 16
5876-4321 Depth = 30 H = 22
56724138- Depth = 30 H = 24
26745138- Depth = 30 H = 22
8674-5123 Depth = 30 H = 16
5476-2381 Depth = 30 H = 24
57-426381 Depth = 30 H = 24
5274-6381 Depth = 30 H = 22
57-436821 Depth = 30 H = 22
251368-47 Depth = 30 H = 18
37-462581 Depth = 30 H = 20
37246158- Depth = 30 H = 18
76534281- Depth = 30 H = 18
5764-2381 Depth = 30 H = 24
-76854123 Depth = 30 H = 16
76-854123 Depth = 30 H = 14
5634-2781 Depth = 30 H = 16
576248-31 Depth = 30 H = 24
568247-31 Depth = 30 H = 24
56-472381 Depth = 30 H = 24
-87546123 Depth = 30 H = 20
87-546123 Depth = 30 H = 18
3624-8571 Depth = 30 H = 16
562378-41 Depth = 30 H = 22
5673-2481 Depth = 30 H = 24
567432-81 Depth = 30 H = 24
527368-41 Depth = 30 H = 22
-51268347 Depth = 30 H = 20
32841756- Depth = 30 H = 16
-41528637 Depth = 30 H = 18
547268-31 Depth = 30 H = 24
568327-41 Depth = 30 H = 24
5874-6123 Depth = 30 H = 20
38-427516 Depth = 30 H = 18
5678-4123 Depth = 30 H = 16
8671-5324 Depth = 30 H = 16
765814-23 Depth = 30 H = 14
76581423- Depth = 30 H = 16
57-486231 Depth = 30 H = 24
5872-6341 Depth = 30 H = 24
57-386421 Depth = 30 H = 24
-21358467 Depth = 30 H = 16
56721834- Depth = 30 H = 24
65-874123 Depth = 30 H = 16
5871-6324 Depth = 30 H = 20
76583412- Depth = 30 H = 14
-54687123 Depth = 30 H = 18
-57618324 Depth = 30 H = 22
567284-31 Depth = 30 H = 22
54-687123 Depth = 30 H = 20
58-647321 Depth = 30 H = 24
7651-8324 Depth = 30 H = 16
7652-8341 Depth = 30 H = 20
46752138- Depth = 30 H = 24
5672-1348 Depth = 30 H = 24
-57641328 Depth = 30 H = 24
65742138- Depth = 30 H = 24
-47561328 Depth = 30 H = 24
52746138- Depth = 30 H = 22
765281-34 Depth = 30 H = 18
-65874123 Depth = 30 H = 14
38742651- Depth = 30 H = 20
76528134- Depth = 30 H = 20
-47568312 Depth = 30 H = 24
46758231- Depth = 30 H = 24
32-471568 Depth = 30 H = 16
86745231- Depth = 30 H = 22
65748231- Depth = 30 H = 24
54361278- Depth = 30 H = 16
-57628341 Depth = 30 H = 24
6574-8312 Depth = 30 H = 24
765834-12 Depth = 30 H = 16
5874-2361 Depth = 30 H = 22
58746231- Depth = 30 H = 24
5678-2341 Depth = 30 H = 22
56784231- Depth = 30 H = 22
5874-6312 Depth = 30 H = 24
-57648312 Depth = 30 H = 24
567382-41 Depth = 30 H = 24
-47586321 Depth = 30 H = 24
Total times: 181441
Total cost: 0.632 second

由结果可知并没有状态的深度可以大于30，且曼哈顿距离与深度的关系也并非简单的线性关系，这说明还有更为准确的算法可以对状态进行估值计算，最近时间有限不再深入研究。

现在有理由认为八数码问题的极限为移动30次。

​