一次“不太顺利”的 PAT 考试经历

发表于

从浙大数据结构MOOC入坑PAT以来，PAT可能是我刷过题目数量最多的OJ了。

下面讲讲我的心路历程吧。

从很久之前就听说PAT甲级可以在一年内1:1等同于浙江大学计算机类专业复试上机考试成绩，直到大二下学期我的专业也开设了数据结构这门课。我是同时跟着学校与MOOC进行，由于学校里的课用的教材是算法导论，里面内容的顺序正好与浙大MOOC相反，所以当学期中的时候我就基本都学完了，进度还算挺快的。

拼题A应该算是我第一次正式接触OJ吧，跟着进度把MOOC配套的OJ刷完了还挺充实的（一开始想用Java，结果OJ第一题就让我超时，优化半天无果后改用C。学期结束后简单学了一下C++，便用C++开始了我的PAT-Advanced刷题之旅。最大的感受就是编程的熟练度有了很大的提高，算法题只要有思路写得越来越快……就想着正好刚学完，去考一下PAT试试吧。我现在考试到我考研并不是在规定的一年期之内，但我也不是冲着这个去的，只是想检验一下自己，顺便积累一下上机编程考试的经验。

于是便有了我这不太顺利的考试过程……

关于考点

辽宁的考点只有一个——沈阳的东北大学计算中心，然后八月底被通知说考试地点改到了东北大学浑南校区，查了一下立马把票改到了沈阳南站。沈阳南站离浑南校区是真的近，打车起步价就能到，不过因为我是第一次去不太熟悉周边交通，等公交车等了很久，下了公交车又走了很久emmmm……这里吹一下东北大学浑南校区，距离校区建立已经好几年了，所有建筑以及内饰都跟新的一样（带工学生实名羡慕）。

划重点：性价比最高的到达浑南校区的方式——从沈阳南站打车

到了学校考试地点又再次变更，从信息学院到主教学楼，不过挺近的也无所谓了。下午1:30考试，提前5分钟才允许进考场。由于还有近一小时的时间，我在考场隔壁教室找了个位置看了一会书（整个教室就我一个人，不太明白为啥几十号人在外面走廊站着等）。

这里有个小技巧：只要时间到了1:30直接刷新页面就可以开始考试了。我们那场因为老师也不知道，所有人干等了三四分钟……

关于考试

机房提供VS2010，dev cpp这两种C++编辑器，因为我一直都用的是VS2019，所以选择了VS。我这时候才发现版本不一样区别是真的大，有些平时一直用的语法到了VS2010上就报错（还是那种抽象得让人看不懂的报错），再加上考场上紧张+第一题不会做，低级语法错误频犯……一个多小时了我第一题还没写出来，心态有点小崩，就跳过去做后面的了，还好后面三题都比较简单。

PAT规则里有写考试最后十分钟系统崩溃后果自负，没想到这不只是说说而已的。大概16:13的时候服务器崩了，无法提交代码，而我这时候刚刚写完第四题还没来得及提交，心态又有点崩了。样例可以过，但是能不能AC心里也没底，服务器崩了题也没法看，就这么干等了20多分钟。考试结束后浙大那边重启了一下服务器，然后给加了15分钟时间提交代码，忐忑地提交了我的第四题，AC！卧槽，贼高兴，没做出来的第一题也没心情看了，直接交卷走人，80分。

关于证书

考完试老师给了三个选项——现场等证书、日后邮寄证书、不要证书。由于不急着回去，就边逛校园边等证书了。

然而证书出的太慢了，我在东大等到七点都没拿到，据老师说浙大服务器这9kb/s的速度下载完成还得1小时……最后留了地址让老师帮忙寄回学校的。

推荐考完留地址直接走人，证书当天等也等不出来。

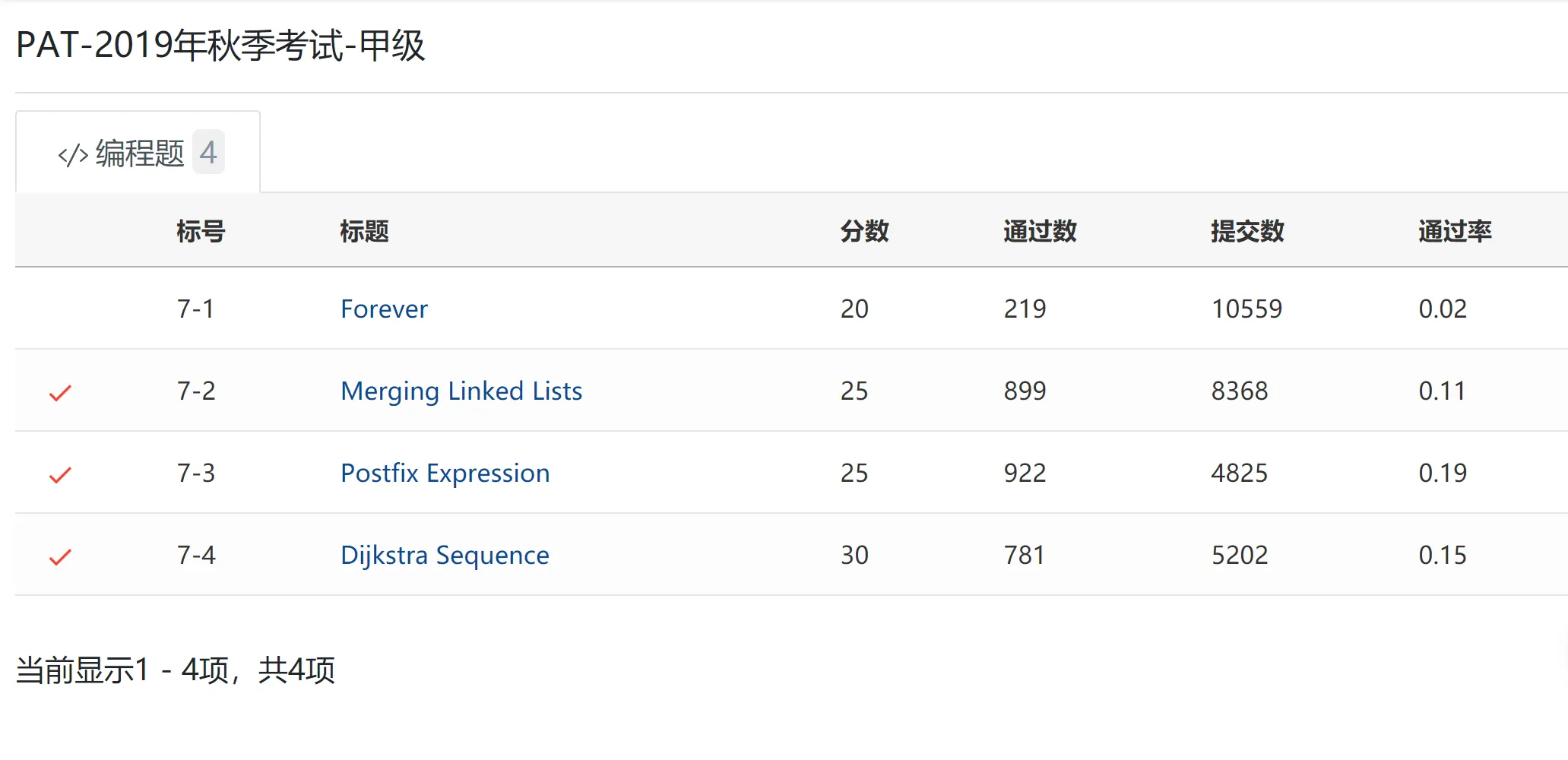
提交统计

考试题目

7-1 Forever (20分)

作者: 陈越 单位: 浙江大学

时间限制: 3000 ms 内存限制: 64 MB 代码长度限制: 16 KB

“Forever number” is a positive integer A with K digits, satisfying the following constrains:

  • the sum of all the digits of A is m;
  • the sum of all the digits of A+1 is n; and
  • the greatest common divisor of m and n is a prime number which is greater than 2.

Now you are supposed to find these forever numbers.

Input Specification:

Each input file contains one test case. For each test case, the first line contains a positive integer N (≤5). Then N lines follow, each gives a pair of K (3<K<10) and m (1<m<90), of which the meanings are given in the problem description.

Output Specification:

For each pair of K and m, first print in a line Case X, where X is the case index (starts from 1). Then print n and A in the following line. The numbers must be separated by a space. If the solution is not unique, output in the ascending order of n. If still not unique, output in the ascending order of A. If there is no solution, output No Solution.

Sample Input:

1
2
3
2
6 45
7 80

Sample Output:

1
2
3
4
5
6
7
8
9
10
11
12
Case 1
10 189999
10 279999
10 369999
10 459999
10 549999
10 639999
10 729999
10 819999
10 909999
Case 2
No Solution

这题恐怖的0.02通过率……原来不是只有我不会啊。

不过我考试的时候是真没有看到那个3000 ms的时限，只是一心想着这种数量级的不可能用穷举，但别的方法我又花了大把时间还没能实现出来。早知道就写个穷举得15分了，还是经验不足。

Solution

点击展开 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>

using namespace std;
struct node {
    int n, A;
};

bool cmp(const node &a, const node &b) {
    if (a.n == b.n) {
        return a.A < b.A;
    }
    return a.n < b.n;
}

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

bool is_prime(int x) {
    for (int i = (int)sqrt(x) + 1; i > 1; i--) {
        if (x % i == 0) {
            return false;
        }
    }
    return true;
}

int sum_d(int x) {
    int ans = 0;
    while (x != 0) {
        ans += x % 10;
        x /= 10;
    }
    return ans;
}

int main() {
    int N;
    cin >> N;
    for (int i = 1; i <= N; i++) {
        vector<node> v;
        int K, m;
        cin >> K >> m;
        printf("Case %d\n", i);

        int l = pow(10, K - 1) + 99, r = pow(10, K) - 1;
        for (int j = l; j <= r; j += 100) {
            if (sum_d(j) == m) {
                int n = sum_d(j + 1);
                int cd = gcd(m, n);
                if (cd > 2 && is_prime(cd)) {
                    v.emplace_back(node{n, j});
                }
            }
        }
        if (v.empty()) {
            printf("No Solution\n");
        } else {
            sort(v.begin(), v.end(), cmp);
            for (auto &it : v) {
                printf("%d %d\n", it.n, it.A);
            }
        }
    }
    return 0;
}


7-2 Merging Linked Lists (25 分)

作者: 陈越 单位: 浙江大学

时间限制: 400 ms 内存限制: 64 MB 代码长度限制: 16 KB

Given two singly linked lists L1=a1→a2→⋯→an−1→an and L2=b1→b2→⋯→bm−1→bm. If n ≥ 2*m, you are supposed to reverse and merge the shorter one into the longer one to obtain a list like a1→a2→bm→a3→a4→bm−1⋯. For example, given one list being 6→7 and the other one 1→2→3→4→5, you must output 1→2→7→3→4→6→5.

Input Specification:

Each input file contains one test case. For each case, the first line contains the two addresses of the first nodes of L1 and L2, plus a positive N (≤105) which is the total number of nodes given. The address of a node is a 5-digit nonnegative integer, and NULL is represented by -1.

Then N lines follow, each describes a node in the format:

1
Address Data Next

where Address is the position of the node, Data is a positive integer no more than 105, and Next is the position of the next node. It is guaranteed that no list is empty, and the longer list is at least twice as long as the shorter one.

Output Specification:

For each case, output in order the resulting linked list. Each node occupies a line, and is printed in the same format as in the input.

Sample Input:

1
2
3
4
5
6
7
8
00100 01000 7
02233 2 34891
00100 6 00001
34891 3 10086
01000 1 02233
00033 5 -1
10086 4 00033
00001 7 -1

Sample Output:

1
2
3
4
5
6
7
01000 1 02233
02233 2 00001
00001 7 34891
34891 3 10086
10086 4 00100
00100 6 00033
00033 5 -1

Solution

一道很简单的反转链表，考场里找自信的题。

点击展开 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<iostream>
#include<string>
#include<algorithm>
#include<vector>
#include<cmath>
#include<unordered_map>
using namespace std;
struct node {
    int address, data, next, pre;
};
void swap(int& a, int& b) {
    int t = a;
    a = b;
    b = t;
}
int main() {
    //freopen("1.txt","r",stdin);
    unordered_map<int, node> ans;
    int l1, l2, N;
    cin >> l1 >> l2 >> N;
    for (int i = 0; i < N; i++) {
        node temp;
        temp.pre = -1;
        cin >> temp.address >> temp.data >> temp.next;
        ans[temp.address] = temp;
    }
    int p1 = l1, p2 = l2, n = 1, m = 1;
    while (ans[p1].next != -1) {
        n++;
        ans[ans[p1].next].pre = p1;
        p1 = ans[p1].next;

    }
    while (ans[p2].next != -1) {
        m++;
        ans[ans[p2].next].pre = p2;
        p2 = ans[p2].next;
    }
    if (m >= 2 * n) {
        swap(m, n);
        swap(l1, l2);
        swap(p1, p2);
    }
    int count = 0;
    p1 = l1;
    vector<node> v;
    while (p1 != -1) {
        count++;
        v.push_back(ans[p1]);
        int p1next = ans[p1].next;
        if (count == 2 && p2 != -1) {
            v.push_back(ans[p2]);
            int temp = ans[p2].pre;
            ans[p2].pre = ans[p1].next;
            ans[p1].next = p2;
            p2 = temp;
            count = 0;
        }
        p1 = p1next;
    }
    for (int i = 0; i < v.size() - 1; i++) {
        printf("%05d %d %05d\n", v[i].address, v[i].data, v[i + 1].address);
    }
    printf("%05d %d -1\n", v[v.size() - 1].address, v[v.size() - 1].data);

    return 0;
}

7-3 Postfix Expression (25 分)

作者: 陈越 单位: 浙江大学
时间限制: 400 ms 内存限制: 64 MB 代码长度限制: 16 KB

Given a syntax tree (binary), you are supposed to output the corresponding postfix expression, with parentheses reflecting the precedences of the operators.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the i-th line corresponds to the i-th node) in the format:

1
data left_child right_child

where data is a string of no more than 10 characters, left_child and right_child are the indices of this node’s left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by −1. The figures 1 and 2 correspond to the samples 1 and 2, respectively.
Figure 1 Figure 2

Output Specification:

For each case, print in a line the postfix expression, with parentheses reflecting the precedences of the operators. There must be no space between any symbols.

Sample Input 1:

1
2
3
4
5
6
7
8
9
8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1

Sample Output 1:

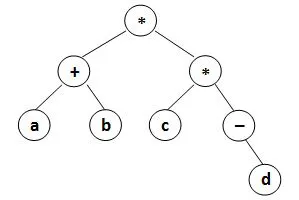
1
(((a)(b)+)((c)(-(d))*)*)

Sample Input 2:

1
2
3
4
5
6
7
8
9
8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1

Sample Output 2:

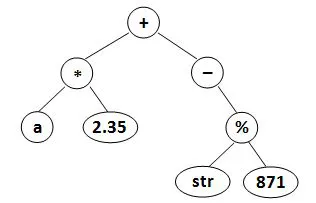
1
(((a)(2.35)*)(-((str)(871)%))+)

Solution

跟1130 Infix Expression几乎一模一样…

最巧的是1130是我考前一天晚上最后刷的一道题，DFS直接解决，注意根据题意加个判断条件。

点击展开 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<iostream>
#include<string>
#include<algorithm>
#include<vector>
#include<cmath>
#include<unordered_map>
using namespace std;
struct node {
    string data;
    int left, right;
};
vector<node> ans;
string s;
void dfs(int cur) {
    s += "(";
    if (ans[cur].left != -1 && ans[cur].right != -1) {
        if (ans[cur].left != -1) {
            dfs(ans[cur].left);
        }
        if (ans[cur].right != -1) {
            dfs(ans[cur].right);
        }
        s += ans[cur].data;
    }
    else {
        if (ans[cur].left != -1) {
            dfs(ans[cur].left);
        }
        s += ans[cur].data;
        if (ans[cur].right != -1) {
            dfs(ans[cur].right);
        }
    }
    s += ")";
}
int main() {
    int n;
    cin >> n;
    node v;
    ans.push_back(v);
    for (int i = 0; i < n; i++) {
        node temp;
        cin >> temp.data >> temp.left >> temp.right;
        ans.push_back(temp);
    }
    bool* isroot = new bool[n + 1];
    fill(isroot, isroot + n + 1, true);
    for (int i = 1; i <= n; i++) {
        if (ans[i].left != -1) {
            isroot[ans[i].left] = false;
        }
        if (ans[i].right != -1) {
            isroot[ans[i].right] = false;
        }
    }
    int root;
    for (int i = 1; i <= n; i++) {
        if (isroot[i]) {
            root = i;
            break;
        }
    }
    dfs(root);
    cout << s;
    return 0;
}

7-4 Dijkstra Sequence (30 分)

Dijkstra’s algorithm is one of the very famous greedy algorithms. It is used for solving the single source shortest path problem which gives the shortest paths from one particular source vertex to all the other vertices of the given graph. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

In this algorithm, a set contains vertices included in shortest path tree is maintained. During each step, we find one vertex which is not yet included and has a minimum distance from the source, and collect it into the set. Hence step by step an ordered sequence of vertices, let’s call it Dijkstra sequence, is generated by Dijkstra’s algorithm.

On the other hand, for a given graph, there could be more than one Dijkstra sequence. For example, both { 5, 1, 3, 4, 2 } and { 5, 3, 1, 2, 4 } are Dijkstra sequences for the graph, where 5 is the source. Your job is to check whether a given sequence is Dijkstra sequence or not.

Input Specification:

Each input file contains one test case. For each case, the first line contains two positive integers Nv (≤103) and Ne (≤105), which are the total numbers of vertices and edges, respectively. Hence the vertices are numbered from 1 to Nv.

Then Ne lines follow, each describes an edge by giving the indices of the vertices at the two ends, followed by a positive integer weight (≤100) of the edge. It is guaranteed that the given graph is connected.

Finally the number of queries, K, is given as a positive integer no larger than 100, followed by K lines of sequences, each contains a permutationof the Nv vertices. It is assumed that the first vertex is the source for each sequence.

All the inputs in a line are separated by a space.

Output Specification:

For each of the K sequences, print in a line Yes if it is a Dijkstra sequence, or No if not.

Sample Input:

1
2
3
4
5
6
7
8
9
10
11
12
13
5 7
1 2 2
1 5 1
2 3 1
2 4 1
2 5 2
3 5 1
3 4 1
4
5 1 3 4 2
5 3 1 2 4
2 3 4 5 1
3 2 1 5 4

Sample Output:

1
2
3
4
Yes
Yes
Yes
No

Solution

这题其实就是写一个Dijkstra用来判断他给的序列，每一步找出所有符合要求的点，如果序列当前位置的点也符合要求，那就用给定的点进行下一步Dijkstra，否则输出No。

点击展开 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<iostream>
#include<string>
#include<algorithm>
#include<vector>
#include<cmath>
#include<unordered_map>
#define inf 99999
#define maxN 1010
using namespace std;
int g[maxN][maxN], dist[maxN];
bool visited[maxN];
int main() {
    int n, m, k;
    cin >> n >> m;
    fill(g[0], g[0] + maxN * maxN, inf);
    for (int i = 0; i < m; i++) {
        int a, b, d;
        scanf("%d%d%d", &a, &b, &d);
        g[a][b] = g[b][a] = d;
    }
    cin >> k;
    for (int i = 0; i < k; i++) {
        fill(dist, dist + maxN, inf);
        fill(visited, visited + maxN, false);
        bool flag = false;
        vector<int> seq(n);
        for (int j = 0; j < n; j++) {
            scanf("%d", &seq[j]);
        }
        dist[seq[0]] = 0;
        for (int j = 0; j < n; j++) {
            flag = false;
            int cur = seq[j], u = -1, min = inf;
            for (int v = 1; v <= n; v++) {
                if (!visited[v] && dist[v] < min) {
                    min = dist[v];
                    u = v;
                }
            }
            if (u == -1) {
                break;
            }
            for (int v = 1; v <= n; v++) {
                if (!visited[v] && dist[v] == min && v == cur) {
                    flag = true;
                    break;
                }
            }
            if (flag) {
                visited[cur] = true;
                for (int v = 1; v <= n; v++) {
                    if (g[cur][v] != inf && dist[v] > dist[cur] + g[cur][v]) {
                        dist[v] = dist[cur] + g[cur][v];
                    }
                }
            }
            else {
                break;
            }
        }
        flag ? printf("Yes\n") : printf("No\n");
    }
    return 0;
}

后记

说起来这次考试发挥并不是很好，在陌生上机环境遇到了很多意料之外的问题，比如以下几点：

  • Win7 的 console 没法直接 Ctrl + V
  • debug 的自动变量窗口关掉不知道怎么调出来(找了十分钟)
  • VS2010 的 console 总是一闪而过（项目子系统设置为控制台也没用）
  • 考场机房的VS2010毫无自动补全功能（缩进、括号的另一边都要自己打，特别不习惯，但是我也没时间去找在哪设置）
  • ……

令我意外的是旁边人啪啦啪啦敲键盘对我没有造成任何影响，看来我抗干扰能力还挺强的 2333，不过这一趟也学到不少东西，值回票价~